This part of the package was written using the S-function formalism (see the Simulink reference manual) and is activated by the startneuro M-file (i.e., by entering the command startneuro at the Matlab prompt). The following window will then appear on the screen.
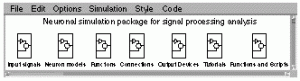
The icons entitled “Input Signals”, “Neuron models”, “Functions”, “Connections”, and “Output devices” contain building blocks which allow to constitute models such as the one shown in the next figure. The icon entitled “Tutorials” allows to access the tutorials described in the next section, while the “Functions and Scripts” icon provides convienent on-line help on the use of the different Matlab M-files, such as those described in the previous section.
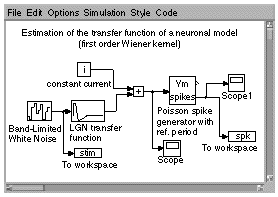
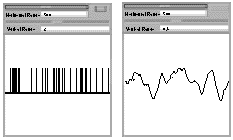
In this example, a band-width limited white noise signal is passed through a linear filter which mimicks the processing performed by an LGN relay cell on its inputs. The resulting output signal is used to drive a Poisson spike train generator. Simulations are started by accessing the “Simulation” pull-down menu (on top) and the resulting spike train as well as the stimulus are stored in two workspace variables (stim and spk, respectively) for subsequent data analysis. The state of the stimulation can be followed by double-clicking on the scope icons, which plot the stimulus and spike train as a function of time (see below).
The subthreshold membrane voltage dynamics of the models is linear and was implemented by numerical integration using a fixed time step. This greatly reduces the programming load but leads to relatively slow simulations. More sophisticated algorithms are described in chapter 14 of “Methods in Neuronal Modeling”. Numerical simulation results were checked by comparison with analytical results (see the section on Data Analysis and Theoretical Routines, above), but no benchmark tests were performed to assess precisely the numerical accuracy of these routines. We would also like to caution the user that simulation results can be affected by the time step used, the properties of random number generators and the stability of the linear system simulated.
